Music theory is the toolbox every musician uses and whatever level you’re at you can always learn something new and exciting to add to it. Theory is an essential aspect of music that provides a foundation for understanding the mechanics and structure of music. One of the most useful concepts in music theory is the circle of fifths, which is an invaluable tool for understanding the relationships between musical keys and chords. In this article, we will explore the circle of fifths for beginners and its significance in music theory. Let’s dive in.
What is the circle of fifths?
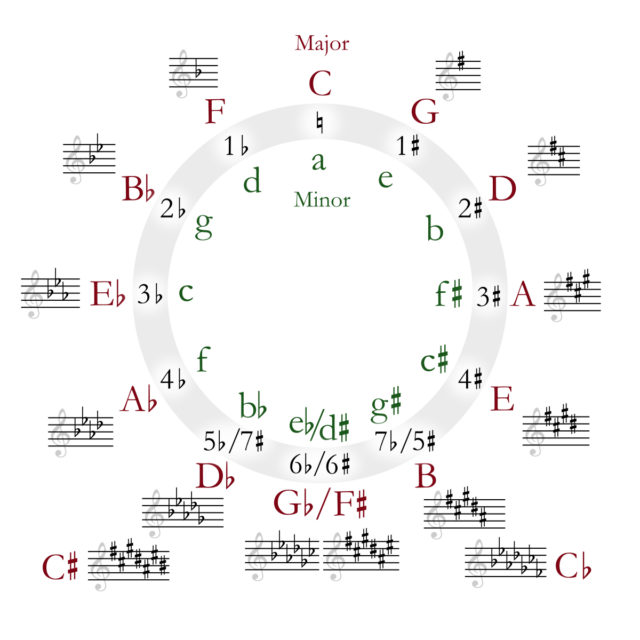
The circle of fifths, or cycle of fifths, is a diagram that illustrates the relationship between the 12 musical keys. It is a circle that is divided into sections representing the 12 notes in western music.
The interactive circle of fifths chart below explains the concept. You can essentially think of it as a music color wheel that shows the key signatures of each of the 12 key centres. As you can see, there are both major and minor circles of fifths.
For example, A minor is the relative minor key of C major, because both scales use a combination of the same notes. By understanding the relative major and minor keys, you can easily transition between major and minor tonalities in your music.
So, if you’re looking for a nice visual representation of the circle of fifths that includes the relative minor keys as well as key signatures on the staff.
What is the origin story of the circle of fifths?
The concept of the circle of fifths can be traced back to the work of the medieval music theorist Guido of Arezzo, who is credited with the invention of the modern musical staff and the solfeggio system. However, the actual circle diagram as we know it today was not formalized until the 18th century by the German musician Johann David Heinichen.
Heinichen was a composer, theorist, and music director who worked in Dresden during the early 18th century. In his treatise “Der Generalbass in der Composition,” which was published in 1728, Heinichen introduced a diagram that showed the relationships between the 12 major and minor keys, based on the pattern of ascending fifths.
Over time, other musicians and theorists refined the circle of fifths, adding new elements and using them to explore various aspects of composition. Today, the circle of fifths remains an important tool for musicians and music educators, and it continues to inspire new research and exploration.
Why is the circle of fifths important?
The circle of fifths is an extremely useful tool for anybody interested in learning about music. Despite its initial appearance of complexity, it is actually rather simple to use once you get the feel of it. For beginners, the Circle of fifths is an ideal way to learn the amount of sharps and flats in a specific key signature, as well as how different keys relate to one another.
Making key changes, chord progressions and harmonizing more understandable. It allows you to quickly discover similar keys for seamless transitions when composing and makes it easier to find common chord patterns utilized in many tunes. In practice, it’s a shortcut for creating effective improvisations, seamlessly transposing compositions and learning which notes go well together.
Circle of fifths chart
Here’s the Circle of fifths diagram from Pianolit. Take a look at how it’s laid out. Notice how the keys travel in fifths as you move clockwise, adding sharps and counterclockwise, introducing flats. Try and count around the circle to see the pattern in action and note how closely similar keys are placed next to each other.
Basic building blocks of the circle of fifths
Before we start using the circle of fifths let’s look at its fundamental building blocks and how to put them into practice.
Understanding the perfect fifth
A perfect fifth is one of the most fundamental intervals in music, forming the basis of the circle of fifths. It spans seven semitones, or five letter names, from the starting note. For example, if you start on C, counting up five letter names (C-D-E-F-G) lands you on G, which is a perfect fifth above C. To find a perfect fifth on the piano, start on any note and count seven semitones [adjacent keys) up.

In the circle of 5ths, each key moves up by a perfect fifth clockwise. This pattern is the foundation of many chord progressions, key changes, and harmonies, making it an essential concept for musicians to master.
Building the sharp keys around the circle
The right-hand side of the circle of fifths chart shows the sharp keys, starting with G major and moving clockwise in perfect fifths. Each step adds one sharp to the key signature.
To memorize this order, use the mnemonic:
Father Charles Goes Down And Ends Battle
If a key has one sharp (G major) we count one letter up the mnemonic ‘Father’ and know that this key has and F#:
G A B C D E F# G
If we want to know what sharps A major has we see on the circle of fifths that it has three sharps Father Charles Goes ( F# C# and G#) creating the A major scale:
A B C# D E F# G# A
Building the flat keys around the circle
On the left-hand side of the circle of 5ths chart, the flat keys appear in perfect fourths (a reverse/anticlockwise perfect fifth) Each step counterclockwise adds one flat to the key signature.
A helpful mnemonic is:
Battle Ends And Down Goes Charles Father
If a key has one flat (Bb major), you count one letter down the mnemonic ‘Battle’ and know that it has a Bb. This helps you form the scale:
Bb C D Eb F G A Bb
If you want to know how many flats the key of Eb major has, you refer to the circle of fifths and see that it has three flats ‘Battle Ends And’ (Bb, Eb, Ab). This gives you the Eb major scale:
Eb F G Ab Bb C D Eb
The circle of fifths bass clef and the circle of fifths treble clef both follow this same structure, making it useful across different instruments.
How to use the circle of fifths to play piano
The circle of fifths is a great way to learn piano scales. It can help you see how various keys are connected. Learning scales and keys around the circle of fifths allows you to practice scales in order and progressively add sharps or flats. In this section, we’ll look at how to use the circle of fifths to guide your piano playing while also improving your awareness of key, chords and their connections.
How to play piano scales with the circle of fifths
The circle of fifths piano layout is ideal for learning and playing scales. Once you’ve built a few scales with the methods shown above you will notice that closely related keys are near to each other on the cycle. You may utilize the circle of 5ths to progressively introduce sharps or flats as you progress through the scales, learning the scales in the order that sharps and flats appear. Scales in the circle of fifths progression are useful for developing muscle memory, improving finger technique and training your ear for smooth key transitions.
To further explore how you can create scales with the circle of fifths you can memorise the relationship between relative major and minor keys. Relative major and minor scales are pairs of scales that share the same key signature but start on different root notes; this relationship can be seen on the minor circle of fifths. The relative minor of any major scale starts on the sixth degree of that major scale, while the relative major of a minor scale starts on the third degree of that minor scale.
Despite their different starting points, these pairs contain the same notes, making them “relative” to each other. You can apply the same strategy with these minor scales, learning them in order of the progression of sharps and flats, all while understanding their position to their relative keys and majors. This shows the benefit of knowing the cycle of fourths well!
How to write piano chord progressions with the circle of fifths
The circle of fifths chords provide a shortcut for building strong chord progressions. You can follow the natural movement around the circle of fifths wheel. If you’re writing music, following the circle of fifths chord progressions can help create smooth, stable transitions between chords and avoid awkward key changes. This method works well for both major and minor keys, as well as jazz and pop harmony due to the strong relationships created between chords when the circle of 5th progression is followed.
How to write piano modulations with the circle of fifths
When modulating between keys, the circle of fifths progression provides a roadmap for both smooth and interesting modulations. Since adjacent keys share many common tones, the circle of fifths explained makes it easier to shift between keys without jarring jumps. Whether modulating up a perfect fifth, moving to a relative minor, or experimenting with a circle of fifths minor keys, this tool ensures fluid and musical key changes.
The best way to explore this is to experiment by playing piano keys and changing between them. If you add flats or remove sharps (go anti-clockwise round the cycle) you may notice a darker feel to your piano playing. If you add sharps and remove flats (go clockwise) you may notice a brighter sound to your playing.
You can also experiment by making larger jumps clockwise or anticlockwise around the cycle. The smaller the movement the more closely related the key and the larger the jump the more alien your modulation will feel.
How to memorize the circle of fifths
Memorizing the circle of fifths helps with key recognition, transposition and composing music more intuitively. Many musicians use mnemonics to remember the order of sharps and flats. There are many tried and tested ways of memorizing the circle of fifths. Lots of people like to use mnemonics, like the ones we looked at before, to memorize the order of key signatures and the order of sharps and flats.
- The sharp keys can be memorized using the following mnemonic: Go Down And Eat Bread, Father
- For example, the third word in the mnemonic is and, which represents the note / key A in the circle of fifths.
- The flat keys can be memorized using the following mnemonic: Friends Be Excellent At Doing Good
- For example, the third word in the mnemonic is excellent, which represents the note / key E in the circle of fourths.
- To make sure you’re internalising the cycle it’s best to play it on piano with the chart. This will ensure you have the right sharps and flats to go along with these mnemonics.
To practice playing piano triads around the cycle of fifths, check out this lesson on Skoove, which also includes the Michael Jackson song ‘Heal the World’.
Conclusion – how will the circle of fifths help me?
The circle of fifths is an invaluable tool for any musician. It helps you understand the relationships between keys, chords and scales. The circle of 5ths chart provides a clear visual reference for key signatures and smooth transitions, whether you’re learning piano, writing music, or improving your improvisation skills.
For any pianist, the piano circle of fifths is especially helpful when practicing chord progressions, modulations and scales. Understanding how major and minor keys connect through the circle of fifths wheel allows you to navigate music theory naturally with confidence.
With some regular practice and help of our helpful mnemonics, you’ll find that using the music circle of fifths becomes second nature. You’ll soon see how it transforms your approach to music. Happy Practicing!
Author of this blog post:
Matthew Dickman

With over a decade of experience in music education Matthew holds a BA in Music from Paul McCartney’s LIPA and an MA in Composition from the University of Salford. Mathew has developed a distinctive compositional voice and approach to music theory education through his research and work in the music industry. Matthew’s writing for Skoove combines experience from orchestral and media composition, and as a gigging jazz musician, to create a wholistic and accessible pedagogy for musicians of any level. Away from music, he enjoys reading and exploring nature to expand his horizons and knowledge contributing to his holistic teaching style.