La teoría musical puede ser un tema intimidante para muchos músicos. Sin embargo, es un aspecto esencial de la música que proporciona una base para comprender la mecánica y la estructura de la música. Uno de los conceptos más importantes de la teoría musical es el círculo de quintas, una herramienta útil para comprender las relaciones entre las tonalidades musicales y los acordes. En este artículo exploraremos el círculo de quintas y su importancia en la teoría musical.
- Enamórate de la música — Aprende tus canciones favoritas; ya sea música clásica, pop, jazz o de cine, todo a un nivel que se adapte a ti.
- Disfruta de interactivas lecciones de piano — Aprende con los cursos que te ayudarán a dominar todo, desde teoría de la música, acordes, técnica y más.
- Obtén retroalimentación en tiempo real — Mejora tu práctica con comentarios enriquecidos mientras Skoove escucha tu forma de tocar y destaca lo que salió bien y las áreas de mejora.
Puntos clave
El círculo de quintas es un diagrama que muestra las relaciones entre las distintas tonalidades musicales.
Se construye a partir de intervalos de quinta perfecta, que constan de 7 semitonos o medios tonos.
El círculo de quintas es una herramienta esencial para que músicos y compositores comprendan las relaciones armónicas entre las tonalidades mayores, modulen con eficacia y creen progresiones de acordes.
Memorizar el círculo de quintas puede ser útil, pero es más importante comprender los conceptos que lo sustentan y cómo utilizarlo eficazmente.
El círculo de quintas se inventó para ayudar a los músicos y compositores a comprender las relaciones entre las distintas tonalidades y crear progresiones armónicas eficaces.
¿Qué es el círculo de quintas?
El círculo de quintas es un diagrama que ilustra la relación entre las 12 tonalidades musicales. Se trata de un círculo dividido en 12 secciones, cada una de las cuales representa una tonalidad diferente. El círculo está dispuesto en el sentido de las agujas del reloj, con la tonalidad de Do mayor en la parte superior y la de Fa# mayor en la inferior. Cada sección del círculo representa una tonalidad musical y sus correspondientes acordes mayores y menores.
El gráfico interactivo del círculo de quintas que aparece a continuación explica el concepto. En esencia, puedes pensar que se trata de una rueda de colores que muestra la progresión de las tonalidades y cuántos sostenidos o bemoles hay en cada tonalidad. Como puedes ver, hay círculos de quintas mayores y menores.
Por ejemplo, La menor es la tonalidad menor relativa de Do mayor, porque ambas escalas utilizan las mismas notas pero en distinto orden. Si conoces las tonalidades menores relativas, podrás pasar fácilmente de tonalidades mayores a menores en tu música. Si buscas una buena representación visual del círculo de quintas que incluya las tonalidades menores relativas y las armaduras del pentagrama, echa un vistazo a esta herramienta interactiva de Pianolit. Es una forma estupenda de explorar las relaciones entre las tonalidades mayores y menores relativas y mejorar tu comprensión de la música.
¿Cuál es el origen del círculo de quintas?
El concepto del círculo de quintas se remonta a la obra del teórico musical medieval Guido de Arezzo, a quien se atribuye la invención del pentagrama musical moderno y del sistema de solfeo. Sin embargo, el diagrama circular tal y como lo conocemos hoy no fue formalizado hasta el siglo XVIII por el músico alemán Johann David Heinichen.
Heinichen fue un compositor, teórico y director musical que trabajó en Dresde a principios del siglo XVIII. En su tratado «Der Generalbass in der Composition», publicado en 1728, Heinichen introdujo un diagrama que mostraba las relaciones entre las 12 tonalidades mayores y menores, basado en el patrón de quintas ascendentes.
Con el tiempo, otros músicos y teóricos perfeccionaron el Círculo de Quintas, añadiendo nuevos elementos y utilizándolo para explorar diversos aspectos de la composición. Hoy en día, el Círculo de Quintas sigue siendo una herramienta importante para músicos y educadores musicales, y continúa inspirando nuevas investigaciones y exploraciones.
Elementos básicos del círculo de quintas
Un intervalo es la distancia entre dos notas cualesquiera. Los intervalos pianísticos son la forma de relacionar las notas del teclado entre sí, y suelen medirse en semitonos o medios tonos. Un semitono es la diferencia entre dos teclas adyacentes, ya sean blancas o negras. Por ejemplo, la distancia de Do a Do♯ es un semitono (o un medio tono), al igual que la distancia de Mi a Mi♭.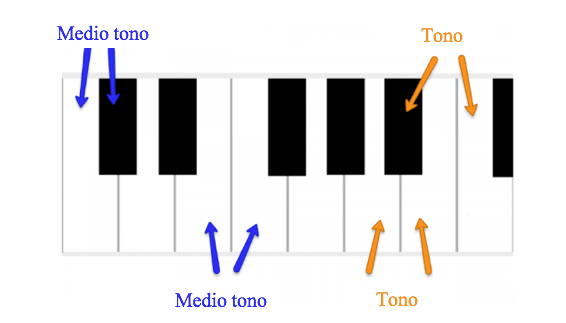
Practica contando algunos intervalos en el teclado. Por ejemplo, un intervalo de 3ª mayor equivale a cuatro semitonos (o cuatro medios tonos). Empieza en Do central, luego cuenta 1 (Do♯), 2 (Re), 3 (Re♯) y 4 (Mi). Do – Mi es un intervalo de tercera mayor. Ahora utiliza este mismo método para encontrar un intervalo de 3ª mayor por encima de Re, Fa y Sol.
El intervalo de 3ª mayor sobre Re es Fa♯ (empieza en Re y cuenta 1 (Re♯), 2 (Mi), 3 (Fa), 4 (Fa♯).
El intervalo de 3ª mayor sobre Fa es La (empieza en Fa y cuenta 1 (Fa♯), 2 (Sol), 3 (Sol♯), 4 (La).
El intervalo de 3ª mayor por encima de Sol es Si (empieza en Sol y cuenta 1 (Sol♯), 2 (La), 3 (La♯), 4 (Si).
Pensamos en ellos de dos maneras: por nombre de nota y por distancia de semitono/medio tono. En términos sencillos, una 2ª es cuando pasamos de una nota a la siguiente, de La a Si. Una 5ª es cuando nos alejamos 5 notas. La forma más sencilla de hacerlo es extender la mano derecha y contar desde el pulgar. Esto funciona incluso si no estás en la misma tonalidad, o en una tonalidad nueva.
La – Si – Do – Re – Mi
Así, una 5ª por encima de La es Mi.
Y si quieres poner en práctica estas ideas sobre los intervalos, tenemos la lección perfecta para ti en Skoove: prueba esta lección interactiva que es una guía paso a paso de la escala de Do mayor antes de enseñarte la canción de Billy Joel «Piano Man»
Entender la quinta perfecta
Ahora puedes utilizar tus conocimientos sobre intervalos para construir un círculo de quintas.
En primer lugar, tienes que entender qué es un intervalo de quinta perfecta: consta de 7 semitonos. Llamamos perfectos a estos intervalos porque la relación entre los dos tonos puede expresarse como un número racional. Por ejemplo, la relación de frecuencias entre los dos tonos en un intervalo de quinta perfecta es 3:2.
Practiquemos contando algunos intervalos de quinta perfecta en el teclado, lo cual es fácil de hacer porque suele coincidir con la posición natural del primer y el quinto dedo. Por ejemplo, si colocas el pulgar de la mano derecha en Do central, el quinto dedo está naturalmente en Sol. Si cuentas de Do a Sol, verás que hay 7 semitonos entre los dos tonos. Esto no sucede siempre, pero es un buen punto de partida.
Ahora practica contando intervalos de quinta perfecta empezando por Re, Sol, Si y Mi♭…
- Empezando por Re, cuenta Re ♯ (1), Mi (2), Fa (3), Fa♯ (4), Sol (5), Sol ♯ (6) y La (7). De Re a La es una quinta perfecta.
- Empezando por Sol, cuente Sol♯ (1), La (2), La♯ (3), Si (4), Do (5), Do♯ (6) y Re (7). De Sol a Re es una quinta perfecta.
- Empezando por Si, cuenta Do (1), Do♯ (2), Re (3), Re♯ (4), Mi (5), Fa (6), Fa♯ (7). De Si a Fa♯ es una quinta perfecta. He aquí un ejemplo en el que la regla del primer al quinto dedo no da como resultado una quinta perfecta.
- Empezando por E♭, cuente E♮ (1), F (2), G♭ (3), G♮ (4), A♭ (5), A♮ (6), B♭ (7). E♭ a B♭ es una quinta perfecta.
Construcción de las armaduras con sostenidos alrededor del círculo
Empiece dibujando un círculo grande en el papel del pentagrama. Tiene que ser lo bastante grande para que quepan los doce tonos, así que calcula correctamente. No te preocupes si el círculo no es perfectamente redondo. Después de dibujar el círculo, marque doce puntos uniformemente espaciados alrededor del círculo.
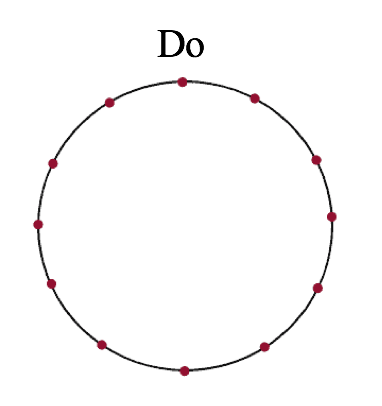
Marca la nota «Do» en la parte superior del círculo (arriba). Es más fácil empezar el círculo desde Do mayor porque la tonalidad de Do mayor tiene cero sostenidos y cero bemoles, sólo las teclas blancas del piano.
- Cuenta 7 semitonos por encima de Do. Puedes utilizar tu teclado si estás cerca, de lo contrario puede ser útil escribir los doce tonos en orden.
- Sol está 7 semitonos por encima de Do. Marca «Sol» una posición a la derecha de Do. También puedes tocar con la mano izquierda para que el círculo de quintas de la clave de fa te sirva. Ahora ya tienes dos claves.
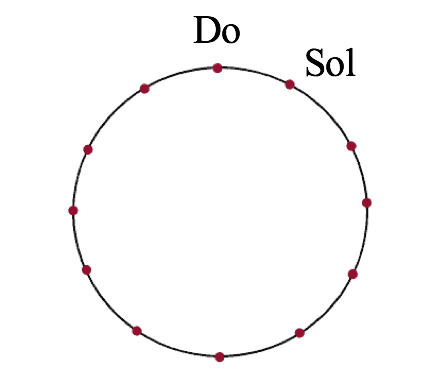
- Cuenta 7 semitonos hacia arriba desde Sol. Si lo has hecho correctamente, llegarás a Re. Marca «Re» una posición a la derecha de «Sol» en el círculo.
- Cuente otros 7 semitonos hacia arriba desde «Re» hasta llegar a «La». Marca «La» una posición en el sentido de las agujas del reloj alrededor del círculo desde «Re».
- Cuenta 7 semitonos hacia arriba desde La hasta llegar a Mi.
- Cuenta 7 semitonos hacia arriba desde Mi hasta llegar a Si.
Ahora deberías tener 8 posiciones marcadas en el círculo de quintas.
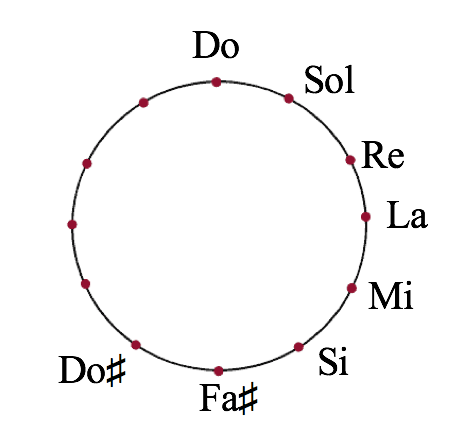
- En la parte superior, la tonalidad de Do mayor no tiene sostenidos ni bemoles.
- La tonalidad de Sol mayor tiene 1 sostenido, Fa♯.
- La tonalidad de Re mayor tiene 2 sostenidos, Fa♯ y Do♯.
- La tonalidad de La mayor tiene 3 sostenidos, Fa♯, Do♯ y Sol♯.
- La tonalidad de Mi mayor tiene 4 sostenidos: Fa♯, Do♯, Sol♯ y Re♯.
- La tonalidad de Si mayor tiene 5 sostenidos, Fa♯, Do♯, Sol♯, Re♯ y La♯.
- La tonalidad de Fa♯ mayor tiene 6 sostenidos, Fa♯, Do♯, Sol♯, Re♯, La♯ y Mi♯.
- Y por último, la tonalidad de Do♯ mayor tiene 7 sostenidos, Fa♯, Do♯, Sol♯, Re♯, La♯, Mi♯, y Si♯…
Observa cómo el nuevo sostenido en cada tonalidad está una quinta por encima del sostenido anterior. Éste es un concepto importante a la hora de aprender a utilizar el círculo de quintas. En el siguiente vídeo se explica con más detalle:
Construcción de las armaduras con bemoles alrededor del círculo
Ahora, junto a «Si», marca el equivalente enarmónico. Recuerda que el equivalente enarmónico significa el mismo tono escrito con un bemol en lugar de un sostenido. El equivalente enarmónico de Si es Do♭. Hacemos esto porque si continuáramos alrededor del círculo con claves sostenidas, terminaríamos marcando dobles sostenidos, que son importantes de conocer, pero innecesariamente complicados cuando se trata del círculo de quintas. Marca este Do♭ en el interior del círculo (ver más abajo).
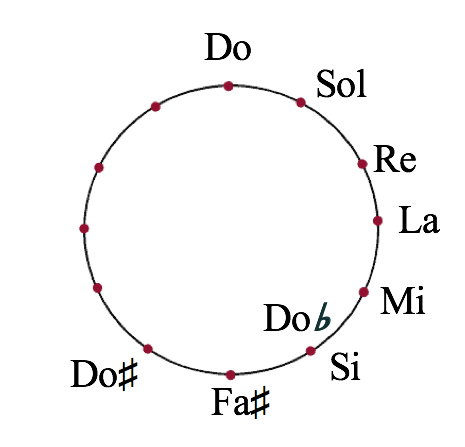
- Cuenta 7 semitonos hacia arriba desde Do♭ hasta llegar a Sol♭
- Cuenta otros 7 semitonos hacia arriba para llegar a Re♭
- Cuenta otros 7 semitonos hacia arriba para llegar a La♭
- Cuenta otros 7 semitonos hasta llegar a Mi♭
- Cuenta otros 7 semitonos hasta llegar a Si♭
- Cuenta otros 7 semitonos hasta llegar a Fa.
- Cuenta otros 7 semitonos hacia arriba y habrás vuelto a casa, a la tonalidad de Do mayor.
¡Ya has construido todo el círculo de quintas!. Estas ocho posiciones representan los bemoles. En el sentido de las agujas del reloj, la tonalidad de Do♭ mayor tiene 7 bemoles: Si, Mi, La, Re, Sol, Do y Fa. El número de bemoles disminuye progresivamente hasta llegar a Do mayor, que tiene cero bemoles.
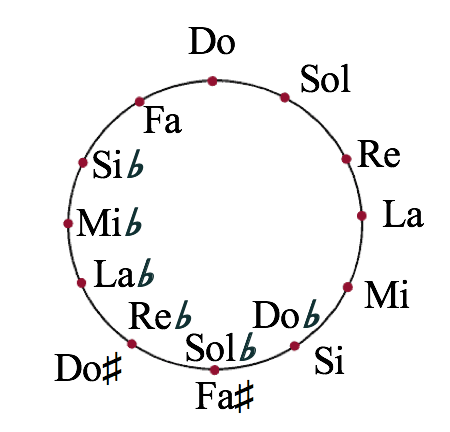
¿Por qué es importante el círculo de quintas?
El círculo de quintas es una poderosa herramienta para cualquier persona interesada en aprender música, a pesar de su apariencia inicial de complejidad. Muchas canciones populares, como «Fly Me To The Moon» de Frank Sinatra y «I Will Survive» de Gloria Gaynor, se basan en el círculo de quintas.
Para los principiantes, el círculo de quintas es una forma excelente de familiarizarse con el número de sostenidos o bemoles de una tonalidad concreta y aprender cómo se relacionan entre sí las distintas tonalidades. Por ejemplo, La menor es el relativo menor de Do mayor. Las tablas del círculo de la 5ª se utilizan en los manuales de música desde los tiempos de J.S. Bach, a principios del siglo XVIII.
Saber utilizar el círculo de quintas es especialmente importante para quienes componen música. Puede ayudar a determinar cómo aplicar diferentes tonalidades en una composición y conducir a nuevos y emocionantes descubrimientos armónicos.
Conclusión: ¿cómo me ayudará el círculo de quintas?
El círculo de quintas es muy importante para cualquier músico, porque mejora la comprensión de los fundamentos básicos de la teoría musical. La relación entre las tonalidades y entre las escalas, así como el modo en que se forman las armaduras, tienen su origen en el círculo de quintas.
Además, muchas progresiones de acordes se basan en el círculo de quintas, por lo que resulta muy útil a la hora de componer canciones. La canción «Always Look on the Bright Side of Life» utiliza una progresión de acordes muy común, ¡y puedes aprenderla aquí en Skoove!
A pesar de que sólo hay 12 nombres de notas diferentes, ¡es increíble la cantidad de formas en que las notas se relacionan entre sí! Aprender a tocar el piano es la mejor manera de poner en práctica la teoría musical que hay detrás del círculo de quintas, así que ¿por qué no empiezas hoy mismo tu prueba gratuita con Skoove?…
La autora de este blog
Alma Gutiérrez es músico, soprano lírica, directora de coro y maestra de piano y teoría musical que actualmente radica en México. Se ha presentado en importantes teatros del norte de México como pianista, corista y solista.Recientemente debutó en las óperas ‘Tosca’ y ‘La Bohème’ de G. Puccini en los roles principales.
