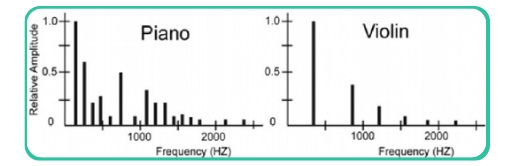
What is a frequency?
In simple terms, frequency refers to the number of sound wave vibrations per second. If there are enough of these vibrations in a second the ear perceives this as a sound we call a pitch. The faster the vibrations, the higher the pitch; the slower the vibrations, the lower the pitch.
For example, the note A4 on the piano has a frequency of 440 Hz. This means the sound wave vibrates 440 times per second.
Our ability to distinguish between different frequencies and combinations is what allows us to hear the difference between a high note and a low note. As a beginner, understanding this relationship will help you play more accurately understand music and develop a better ear.
How do note frequencies relate to piano keys?
On the piano, each key corresponds to a specific frequency.As we know, A4 (the middle A on the keyboard) vibrates at 440 Hz. As you move up the keyboard, the frequency of each note increases. Take a look at this handy frequency chart which shows the piano note frequencies of each key on the keyboard.
| Note | Octave 0 | Octave 1 | Octave 2 | Octave 3 | Octave 4 | Octave 5 | Octave 6 | Octave 7 | Octave 8 |
|---|---|---|---|---|---|---|---|---|---|
| C | 16.35 Hz | 32.70 Hz | 65.41 Hz | 130.81 Hz | 261.63 Hz | 523.25 Hz | 1046.50 Hz | 2093.00 Hz | 4186.01 Hz |
| C#/Db | 17.32 Hz | 34.65 Hz | 69.30 Hz | 138.59 Hz | 277.18 Hz | 554.37 Hz | 1108.73 Hz | 2217.46 Hz | 4434.92 Hz |
| D | 18.35 Hz | 36.71 Hz | 73.42 Hz | 146.83 Hz | 293.66 Hz | 587.33 Hz | 1174.66 Hz | 2349.32 Hz | 4698.63 Hz |
| D#/Eb | 19.45 Hz | 38.89 Hz | 77.78 Hz | 155.56 Hz | 311.13 Hz | 622.25 Hz | 1244.51 Hz | 2489.02 Hz | 4978.03 Hz |
| E | 20.60 Hz | 41.20 Hz | 82.41 Hz | 164.81 Hz | 329.63 Hz | 659.25 Hz | 1318.51 Hz | 2637.02 Hz | 5274.04 Hz |
| F | 21.83 Hz | 43.65 Hz | 87.31 Hz | 174.61 Hz | 349.23 Hz | 698.46 Hz | 1396.91 Hz | 2793.83 Hz | 5587.65 Hz |
| F#/Gb | 23.12 Hz | 46.25 Hz | 92.50 Hz | 185 Hz | 369.99 Hz | 739.99 Hz | 1479.98 Hz | 2959.96 Hz | 5919.91 Hz |
| G | 24.50 Hz | 49 Hz | 98 Hz | 196 Hz | 392 Hz | 783.99 Hz | 1567.98 Hz | 3135.96 Hz | 6271.93 Hz |
| G#/Ab | 25.96 Hz | 51.91 Hz | 103.83 Hz | 207.65 Hz | 415.30 Hz | 830.61 Hz | 1661.22 Hz | 3322.44 Hz | 6644.88 Hz |
| A | 27.50 Hz | 55 Hz | 110 Hz | 220 Hz | 440 Hz | 880 Hz | 1760 Hz | 3520 Hz | 7040 Hz |
| A#/Bb | 29.14 Hz | 58.27 Hz | 116.54 Hz | 233.08 Hz | 466.16 Hz | 932.33 Hz | 1864.66 Hz | 3729.31 Hz | 7458.62 Hz |
| B | 30.87 Hz | 61.74 Hz | 123.47 Hz | 246.94 Hz | 493.88 Hz | 987.77 Hz | 1975.53 Hz | 3951.07 Hz | 7902.13 Hz |
FAQ
Author of this blog post:
Susana Pérez Posada

With over seven years of piano education and a deep passion for music therapy, Susana brings a unique blend of expertise to Skoove. A graduate in Music Therapy from SRH Hochschule Heidelberg and an experienced classical pianist from Universidad EAFIT, she infuses her teaching with a holistic approach that transcends traditional piano lessons. Susana’s writings for Skoove combine her rich musical knowledge with engaging storytelling, enriching the learning experience for pianists of all levels. Away from the piano, she loves exploring new places and immersing herself in a good book, believing these diverse experiences enhance her creative teaching style.
Published by Lydia Ogn from the Skoove team